Providence, RI---In his 1989 book "The Emperor's New Mind", RogerPenrose commented on the limitations on human knowledge with astriking example: He conjectured that we would most likely never knowwhether a string of 10 consecutive 7s appears in the digital expansionof the number pi. Just 8 years later, Yasumasa Kanada used a computerto find exactly that string, starting at the 22869046249th digit ofpi. Penrose was certainly not alone in his inability to foresee thetremendous power that computers would soon possess. Many mathematicalphenomena that not so long ago seemed shrouded and unknowable, can nowbe brought into the light, with tremendous precision.
In their article "Exploratory Experimentation and Computation", toappear in the November 2011 issue of the Notices of the AmericanMathematical Society, David H. Bailey and Jonathan M. Borwein describehow modern computer technology has vastly expanded our ability todiscover new mathematical results. "By computing mathematicalexpressions to very high precision, the computer can discovercompletely unexpected relationships and formulas," says Bailey.
Mathematics, the Science of Patterns
A common misperception is that mathematicians' work consists entirelyof calculations. If that were true, computers would have replacedmathematicians long ago. What mathematicians actually do is todiscover and investigate patterns---patterns that arise in numbers, inabstract shapes, in transformations between different mathematicalobjects, and so on. Studying such patterns requires subtle andsophisticated tools, and, until now, a computer was either too bluntan instrument, or insufficiently powerful, to be of much use inmathematics. But at the same time, the field of mathematics grew anddeepened so much that today some questions appear to requireadditional capabilities beyond the human brain.
"There is a growing consensus that human minds are fundamentally notvery good at mathematics, and must be trained," says Bailey. "Giventhis fact, the computer can be seen as a perfect complement tohumans---we can intuit but not reliably calculate or manipulate;computers are not yet very good at intuition, but are great atcalculations and manipulations."
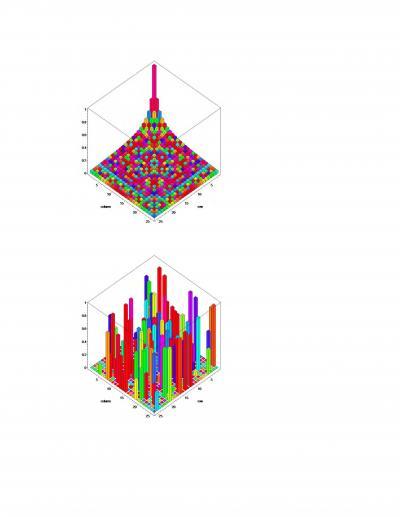
Mathematicians often work with matrices, which are arrays ofnumbers. When written on a page, a matrix can look like a sea ofnumbers, so any patterns that might occur in the numbers can bedifficult to discern. More and more, mathematicians are turning tographical representations of matrices, like the two examples here.By using color and form to indicate the values of the numbers in thematrix, these graphical representations can instantly give a sense ofthe patterns in the matrix. The first picture is a representation of amatrix in which the numbers exhibit a clear pattern; the secondpicture, by contrast, is a matrix in which the numbers are random.
(Photo Credit: Graphic by David Bailey and Jonathan Borwein. Request theirpermission before reproducing the graphic.)
Although mathematics is said to be a "deductive science",mathematicians have always used exploration, whether throughcalculations or pictures, to test ideas and gain intuition, in muchthe same way that researchers in inductive sciences carry outexperiments. Today, this inductive aspect of mathematics has grownthrough the use of computers, which have vastly increased the amountand type of exploration that can be done. Computers are of courseused to ease the burden of lengthy calculations, but they are alsoused for visualizing mathematical objects, discovering newrelationships between such objects, and testing (and especiallyfalsifying) conjectures. A mathematician might also use a computer toexplore a result to see whether it is worthwhile to attempt a proof.If it is, then sometimes the computer can give hints about how theproof might proceed. Bailey and Borwein use the term "experimentalmathematics" to describe these kinds of uses of the computer inmathematics.
Exploring Prime Numbers via Computers
Their article gives several examples of experimental mathematics; thecomputations of the digits of pi mentioned above is one of them.Another example is provided by computer explorations of a mathematicalproblem known as Giuga's Conjecture. This conjecture proposes that,for any positive integer n, one can check definitively whether n isprime by calculating a certain sum in which n appears in the exponentof the summands. That sum would have a certain value, call it S, ifand only if n is prime; stated differently, that sum would not havethe value S if and only if n is composite. Although the conjecturedates to 1950, it has never been proved and seems out of reach byconventional mathematical methods.
However, Bailey and Borwein, along with their collaborators, were ableto use computers to show that any number that is an exception toGiuga's Conjecture must have more than 3,678 distinct prime factorsand be more than 17,168 decimal digits long. That is, any shortercomposite number cannot result in the value S. This does not proveGiuga's Conjecture is true, but it is a compelling piece of evidencein favor of the conjecture's truth. This kind of empirical evidenceis sometimes just what is needed to generate enough confidence for amathematician to dedicate energy to seeking a full proof. Withoutsuch confidence, the inspiration to push through to a proof might notbe there.
Impact on Education
In addition to discussing state-of-the-art uses of computers inmathematics, the article also touches on the need to refashionmathematics education to give students the tools of experimentalmathematics. "The students of today live, as we do, in aninformation-rich, judgment-poor world in which the explosion ofinformation, and of tools, is not going to diminish," says Borwein."So we have to teach judgment (not just concern with plagiarism) whenit comes to using what is already possible digitally. Additionally,it seems to me critical that we mesh our software design---and ourteaching style more generally---with our growing understanding of ourcognitive strengths and limitations as a species."
Source: American Mathematical Society